Muerte cruzada: ¿Ancla o salvavidas?

La muerte cruzada es un mecanismo de destrucción mutua asegurada que busca resolver conflictos entre el Ejecutivo y el Legislativo a través de amenazas bilaterales de disolución. A pesar de las críticas conocidas —como el desequilibrio a favor del Ejecutivo debido a costos nulos de coordinación— este mecanismo tiene también implicaciones electorales que posiblemente no fueron anticipadas por los constituyentes.




Examinemos el caso de Guillermo Lasso, el primer presidente en recurrir al mecanismo de la muerte cruzada. Su decisión se fundamenta en la confluencia de tres factores determinantes: (a) intentos de censura legislativa, (b) desafíos en la ejecución de su programa gubernamental, y (c) una crítica crisis de narcotráfico y violencia. Aunque legalmente los dos primeros elementos ofrecen justificación suficiente para activar el mecanismo de muerte cruzada y convocar a elecciones, es poco plausible que dicho recurso se hubiera ejercido sin la presencia del tercer factor. Este último actuó como un catalizador fulminante, precipitando la decisión ante el caos sin precedentes que instigó en el país.

En este escenario inestable, el período en el poder del nuevo mandatario será de 17 meses y 25 días, extendiéndose desde el 30 de noviembre de 2023 hasta el 24 de mayo de 2025. Teóricamente, el líder electo se encuentra en una especie de lotería electoral tipo winner-take-all: o bien consolida su reelección, ampliando su mandato a un total de 65 meses, o es depuesto después de los 17 meses iniciales. En las siguientes líneas, argumento que esta lotería está inclinada hacia su reelección.

Este sesgo emerge del enfoque bayesiano para la toma de decisiones en contextos inciertos. Supongamos que estamos en la oscuridad respecto a la habilidad del candidato electo para gestionar una crisis. Sin embargo, partimos de una creencia inicial: su habilidad, $\theta$, es una variable aleatoria que puede tomar cualquier valor entre $-\infty$ e $\infty$. Desde nuestra perspectiva, la expectativa de esta variable es cero, expresada como una distribución normal $\theta\sim\mathcal{N}\left(0,\sigma^2/\tau\right)$. Aquí, la varianza $(\sigma^2/\tau)$ actúa como un indicador cuantitativo de nuestra incertidumbre a priori, que podría ser baja (si $\tau>1$) o alta (si $\tau=1$). La figura siguiente muestra que una varianza baja (panel izquierdo) concentra la densidad de probabilidad cerca de nuestra expectativa cero, mientras que una varianza alta (panel derecho) da lugar a una distribución más dispersa y, por ende, más "plana".

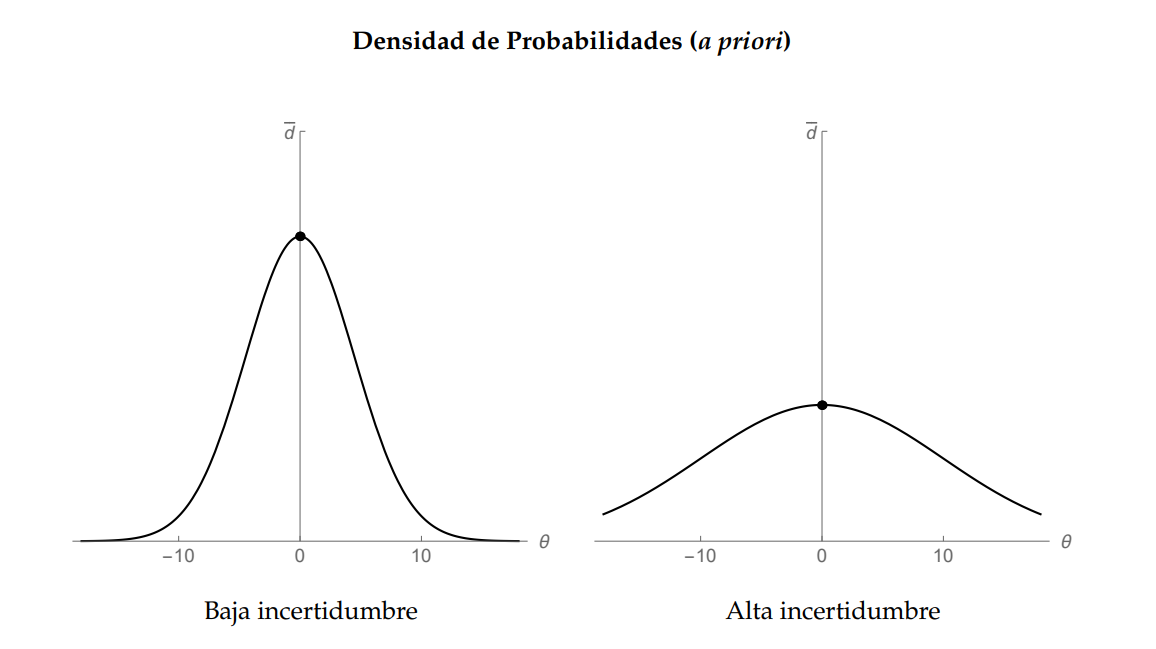
Al asumir su cargo, el candidato electo se enfrenta al reto de gobernar en medio del caos. Su desempeño se manifiesta a través de una señal informativa, $y$, que para nosotros sirve como un indicador de su competencia subyacente—y está modelado como una variable aleatoria normal $y \sim \mathcal{N}(\theta, \sigma^2)$. ¿Cómo actualizamos nuestras creencias iniciales en función de esta señal? Según el Teorema de Bayes, en contextos con elevada incertidumbre a priori, incluso señales ruidosas sobre la habilidad del candidato adquieren una relevancia comparativa mayor. Formalmente, las creencias posteriores, $\hat{\theta}$, son proporcionales al producto de nuestras creencias a priori y la verosimilitud de la señal observada.

Para ilustrar este fenómeno, la figura siguiente muestra cómo una alta varianza en nuestras creencias iniciales puede resultar en disparidades significativas en la actualización de nuestras creencias, dadas las mismas señales de desempeño. Específicamente, nuestra expectativa sobre la aptitud del candidato se desplaza levemente desde el punto de origen cuando la varianza inicial es baja (panel izquierdo), en contraposición a cuando la varianza inicial es alta (panel derecho).

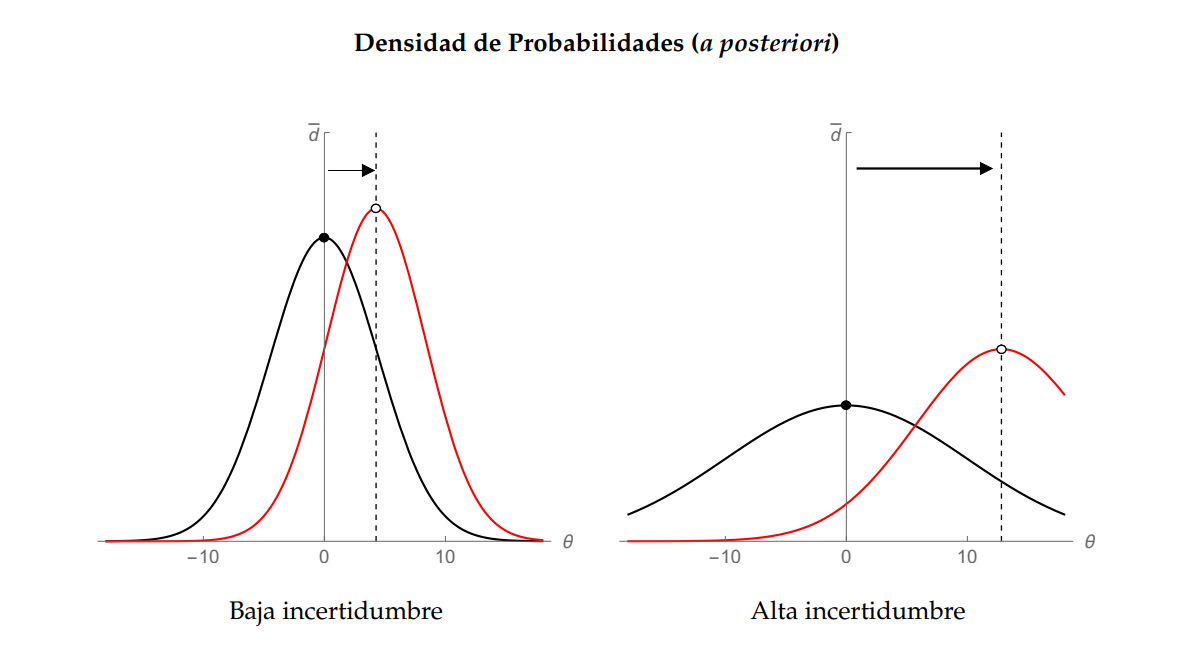
El impacto sustancial de una señal informativa sobre nuestras creencias puede llevar, de manera natural, a retornos electorales no-lineales. Este fenómeno se vuelve particularmente relevante en el contexto del riesgo de selección adversa que enfrentan los votantes al (re)elegir un candidato en circunstancias caóticas. Una posible mitigación para este tipo de inferencias erróneas sería disponer de un mayor número de señales sobre el candidato electo—cuantas más señales tengamos, más precisa será nuestra inferencia. Sin embargo, este enfoque se encuentra obstaculizado por el mecanismo de muerte cruzada, que impone un mandato de duración extra-limitada y, en consecuencia, restringe el número de señales informativas que podrían generarse.

Para abordarlo de forma más rigurosa, introduzcamos una métrica específica de retorno electoral que evalúe el cambio en nuestra utilidad esperada cuando optamos por un candidato en dos escenarios distintos: el primero, caracterizado por nuestras creencias a priori de alta incertidumbre y sin información adicional; y el segundo, en el que disponemos de una serie histórica de desempeños del candidato, denotada como $(y_1,y_2,\ldots,y_n)$. En este marco, definimos nuestra función de utilidad como $-y^2$. Esta elección refleja nuestra premisa de que el candidato ideal minimizaría el caos, lo cual se traduce en una competencia $\theta^*=0$. En contraposición, cualquier candidato con $\theta\neq 0$ nos causa desutilidad en tanto contribuye al caos en lugar de apagarlo. Formalmente, esta medida de retorno equivaldría a

Con esta métrica de retorno electoral, $\Delta(n,\tau)$, podemos explorar cómo la longitud del mandato condiciona el volumen de señales generables y, en consecuencia, nuestra capacidad para realizar inferencias precisas. Para ilustrar este punto, la figura subsiguiente presenta la evolución de dicha métrica en función de una secuencia aleatoria de desempeños del candidato. Específicamente, la figura sintetiza los resultados de $j\in\{1,2,...,100\}$ simulaciones individuales. En cada simulación se realiza lo siguiente: (a) se selecciona de forma aleatoria entre políticos con diversos grados de competencia, y (b) se genera una secuencia aleatoria de desempeños correspondiente al número de meses del mandato, dadas las competencias seleccionadas. [Nota: El código fuente, implementado en Wolfram Mathematica, se encuentra disponible al final de este blog post.]

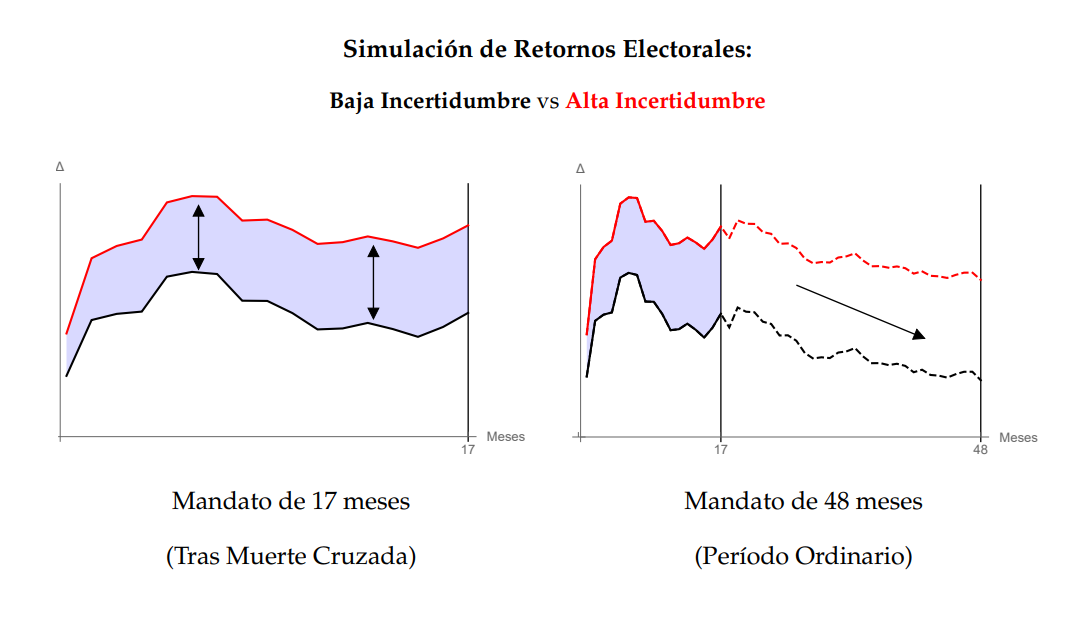
El panel izquierdo simula la evolución de los retornos electorales a medida que se reciben señales informativas $i\in\{1,2,...,17\}$ sobre la competencia del candidato. La disparidad entre las líneas roja y negra representa la bonificación en retornos electorales que el candidato electo recibe debido a la incertidumbre inicial; aquí, la línea negra sirve como un contrafactual donde la única variación es una menor dispersión ($\tau$) en nuestras creencias a priori en comparación con la línea roja. Notablemente, la simulación revela una brecha no trivial que incrementa en magnitud tanto para la línea roja como para la negra.

Por su parte, el panel derecho proporciona otro contrafactual: cómo se habrían comportado los retornos si el mandato del candidato hubiera durado 48 meses en lugar de 17. En este escenario, se simulan señales informativas adicionales $i\in\{18,19,...,48\}$. Para distinguir entre ambos paneles, las líneas en esta figura son discontinuas. Hay dos punto clave. Primero, la tendencia se invierte y el retorno disminuye en ambos casos: aunque las señales iniciales fueron favorables, la acumulación de información adicional afinó nuestras inferencias sobre la competencia del candidato, demostrando ser insuficiente para manejar la crisis, lo que a su vez reduce su retorno. Segundo, la brecha se ensancha aún más, ya que en un contexto de menor dispersión inicial, el descubrimiento de la insuficiente competencia del candidato resulta más costoso. En síntesis, el mensaje primordial es que la elevada incertidumbre inicial puede intensificar el efecto de noticias positivas a corto plazo, resultando en retornos electorales no lineales en favor del candidato electo. Además, la brevedad del mandato aumenta la probabilidad de que mantengamos en el poder a un candidato que, en un escenario contrafactual con un mandato más extenso, habríamos considerado inadecuado a raíz de nuestras inferencias afinadas.

En conclusión, la muerte cruzada, al instaurar un mandato presidencial excepcionalmente corto, restringe nuestras capacidades inferenciales y potencialmente nos induce a mantener en el cargo a líderes que, en un escenario de mandato ordinario, habríamos depuesto. Este efecto se potencia en contextos de alta incertidumbre, donde incluso señales mínimamente informativas pueden crear expectativas desmesuradas. En última instancia, la muerte cruzada podría funcionar como un "gol olímpico" en el ámbito político: un evento excepcional pero decisivo que, dadas las reglas del juego, transforma de manera sustancial la dinámica competitiva en favor del Ejecutivo.

Ahora, mientras que un incremento en el número de observaciones perfecciona nuestra capacidad como cuerpo electoral para destituir a políticos ineficaces, esta acumulación de señales no necesariamente anula la brecha inducida por la variabilidad en la incertidumbre inicial. Formalmente, supongamos que la competencia «verdadera» del candidato electo es $\theta=\theta_V$. En el límite cuando el número de señales se aproxima al infinito, la discrepancia entre los retornos convergerá a



Esta expresión es estrictamente positiva porque $\tau>1$, lo cual indica que aunque la acumulación de información pueda mitigar la brecha en retornos electorales originada por diferencias en incertidumbre inicial, no la elimina por completo. Además, la magnitud de la expresión aumenta exponencialmente con la incompetencia del político (recordemos que el parámetro que maximiza nuestra utilidad es $\theta^*=0$). Intuitivamente, esto se debe a que las noticias desfavorables respecto al candidato son menos perjudiciales cuando la incertidumbre inicial es alta.

Efectivamente, el efecto no-trivial que una señal positiva puede ejercer sobre el rendimiento electoral de un candidato podría incentivarlo a intensificar esfuerzos dirigidos a mejorar el bienestar público. No obstante, se desencadena aquí un dilema: aunque dicho esfuerzo de corto plazo pueda beneficiar a la ciudadanía en el presente, corre el riesgo de exacerbar el problema de selección adversa. En otras palabras, al estimular el esfuerzo inmediato, podríamos inadvertidamente perpetuar la elección de candidatos subóptimos en el contexto del bienestar a largo plazo. Este fenómeno encapsula el trade-off clásico entre riesgo moral y selección adversa, conceptos centrales en la economía política. El riesgo moral concierne al incentivo para el esfuerzo, mientras que la selección adversa aborda la idoneidad intrínseca del candidato.

Para recurrir a una analogía, imagina que la arena política es comparable a un torneo deportivo. Un gol de último minuto puede catapultar a un jugador al estrellato, motivándolo a redoblar esfuerzos en futuros encuentros para mantener su estatus. Este es el poder catalizador de una señal positiva en la política: tiene la capacidad de transformar a un candidato electo en un icono electoral prácticamente de inmediato. Pero ahí reside la paradoja, semejante a un "autogol" ejecutado en cámara lenta. En el fervor de celebrar estos logros a corto plazo, corremos el riesgo de obviar estrategias de largo alcance, tales como la táctica defensiva y el juego colaborativo. Este es el delicado balance entre el riesgo moral y la selección adversa: mientras el primero nos impulsa a buscar triunfos inmediatos, el segundo nos previene de enlistar jugadores inadecuados para una temporada completa. En este escenario, donde la incertidumbre reina y la muerte cruzada actúa como catalizador excepcional, candidatos mediocres podrían fácilmente cosechar los frutos de victorias cortas. Se trata de un atajo pernicioso; después de todo, ¿qué impide que este mecanismo se convierta en una estrategia recurrente, socavando la calidad de la gobernanza a largo plazo?

Concluyendo, mi argumento apunta a que la estructura institucional, aquí ilustrada mediante el concepto de muerte cruzada, tiene implicancias profundas para la estabilidad y eficacia de la gobernanza democrática. En contextos donde la evaluación pública del liderazgo es susceptible a imprecisiones y sesgos, un mecanismo diseñado para dirimir conflictos Ejecutivo-Legislativo podría, de forma paradójica, perpetuar una administración ineficaz o incluso peligrosa.

(* Inicializar parámetros *)
mu1 = mu2 = 0;
t1 = input1; t2 = input2;
n1 = 17; n2 = 48;
sigma2 = input1;
numSimulations = 100;
avgFunctionDList1 = avgFunctionDList2 = ConstantArray[0, n2];

(* Bucle para numSimulations simulaciones *)

Do[
  posteriorMeans1 = {mu1}; posteriorMeans2 = {mu2};
  posteriorVariances1 = {t1}; posteriorVariances2 = {t2};
  functionDList1 = functionDList2 = {};
  
  (* Bucle a través de n2 iteraciones para actualizar el posterior con cada nueva muestra *)

  Do[
    Ability =  RandomChoice[{0, 1, 2, 3}];
    eSample = RandomVariate[NormalDistribution[0, Sqrt[sigma2]]];
    y = Ability + eSample;
  
    (* Actualización bayesiana para la media y varianza del posterior *)

    UpdatePosterior[meanList_, varList_] := Module[{lastMean, lastVar, newMean, newVar},
      lastMean = Last[meanList];
      lastVar = Last[varList];
      newMean = (y/sigma2 + lastMean/lastVar) / (1/sigma2 + 1/lastVar);
      newVar = 1 / (1/sigma2 + 1/lastVar);
      {newMean, newVar}
    ];
  
    {newMean1, newVar1} = UpdatePosterior[posteriorMeans1, posteriorVariances1];
    {newMean2, newVar2} = UpdatePosterior[posteriorMeans2, posteriorVariances2];
  
    (* Calcular la utilidad para cada modelo *)

    ComputeUtility[mean_, variance_] := 
      TransformedDistribution[-(w + e)^2, {w \[Distributed] NormalDistribution[mean, Sqrt[variance]], 
                                            e \[Distributed] NormalDistribution[0, Sqrt[sigma2]]}];
  
    util1 = ComputeUtility[newMean1, newVar1];
    util2 = ComputeUtility[newMean2, newVar2];
  
    (* Calcular D para cada modelo *)

    ComputeD[util_, t_] := (Mean[util] - (-sigma2 - t)) / -(-sigma2 - t);
    DList1 = ComputeD[util1, t1];
    DList2 = ComputeD[util2, t2];
  
    (* Agregar a las listas *)

    AppendTo[posteriorMeans1, newMean1]; AppendTo[posteriorMeans2, newMean2];
    AppendTo[posteriorVariances1, newVar1]; AppendTo[posteriorVariances2, newVar2];
    AppendTo[functionDList1, DList1]; AppendTo[functionDList2, DList2];
  
  , {i, 1, n2}];
  
  avgFunctionDList1 += functionDList1 / numSimulations;
  avgFunctionDList2 += functionDList2 / numSimulations;

, {j, 1, numSimulations}];

(* Graficar los datos simulados *)

yRange = MinMax[Join[avgFunctionDList1, avgFunctionDList2]];


plotFull = 
  ListLinePlot[{avgFunctionDList1, avgFunctionDList2}, 
   PlotStyle -> {{Red, Dashed}, {Black, Dashed}}, 
   AxesLabel -> {"Meses", "\[CapitalDelta]"}, 
   PlotRange -> {{0, n2}, yRange}, 
   Ticks -> {{{n1, ToString[n1]}, {n2, ToString[n2]}, {0, "0"}}, {{0, 
       "0"}, Automatic}}];

plotPartial = 
 ListLinePlot[{Take[avgFunctionDList1, n1], 
   Take[avgFunctionDList2, n1]}, 
  PlotStyle -> {{Red, Solid}, {Black, Solid}}, Filling -> {1 -> {2}}, 
  FillingStyle -> {Directive[Red, Opacity[0.15]], 
    Directive[Blue, Opacity[0.15]]},
  AxesLabel -> {"Meses", "\[CapitalDelta]"}, 
  PlotRange -> {{0, n1}, yRange}, 
  Ticks -> {{{n1, ToString[n1]}, {n2, ToString[n2]}, {0, "0"}}, {{0, 
      "0"}, 0}}, GridLines -> {{17, 48}, {}}, 
  GridLinesStyle -> {{Black}, {Black}}, BaseStyle -> {FontSize -> 14}]

finalPlot = 
 Show[plotFull, plotPartial, 
  PlotLegends -> {"Alta Incertidumbre", "Baja Incertidumbre"}, 
  AxesLabel -> {"Meses", "\[CapitalDelta]"}, 
  Ticks -> {{{n1, ToString[n1]}, {n2, ToString[n2]}, {0, "0"}}, {{0, 
      "0"}, 0}}, GridLines -> {{17, 48}, {}}, 
  GridLinesStyle -> {{Black}, {Black}}, BaseStyle -> {FontSize -> 14}]